みなさんこんにちは!
道路を作るときにキレイにカーブを作るときにみんな使っている、お手頃の土方カーブの説明をします。
縁石や側溝などの曲線を作るときに丁張が細かく立っているわけではないので、作業員の人は土方カーブを使っていきます。
私は初めて土方カーブの名前を聞いたときは、見た目で並べていくことが土方カーブと思っていたら馬鹿にされました。
いくら測量技術が発達しているとは細かく丁張を立てるのは面倒ですし、丁張だらけになると施工の邪魔で必ずぶっ壊れます。
できる作業員の人は丁張が3点あれば勝手に土方カーブを計算して施工してくれます。
丁張が2点しかない場合は計算して出さないといけませんので、さっそく説明を始めますね。
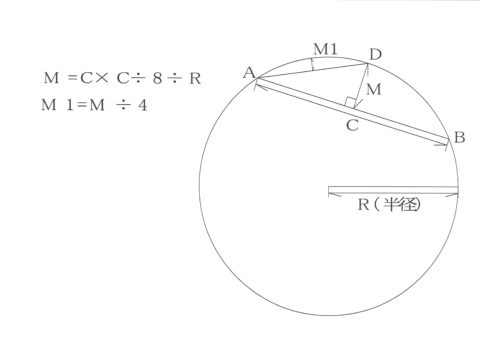
図面上のAとBが丁張だと仮定します。
A~Bの距離を測り、その距離をCとします。
Rは図面に記載されているカーブの半径のことです。
公式は
M=C×C÷8÷R
このように計算しますが、CとかRだとわかりにくいのでもう少し説明を加えます。
A~Bの距離=C
C=20mだとします。
カーブの半径Rが200mだと
M=20×20÷8÷200 このような式になります。
これを計算すると
M=0.25になり、図面上のA~Bの距離の半分の10mところを外側に0.25m出すとDの位置になり、Dをめがけて構造物設置していけばいいです。
一か所出してしまえば、そのあとは
M1=M÷4 になります。
上記の公式で計算するとM1の長さがわかります。これをどんどん計算していけば円に近くなります。
M=25cmですから
25cm÷4=6.25cm
M1=6.25cmになり、約6cm外側に構造物を設置していきます。1cm未満は四捨五入してあとは見た目でキレイなカーブが描けていればOKです。
だだしこの計算でできるのは、だいたい半径100m以上になります。なぜなら、正確な計算ではないので半径Rが10mとかだと誤差が大きすぎて綺麗なカーブになりません。
小さな半径Rで、どうしても正確な数字が欲しい人は次のように計算して下さい。
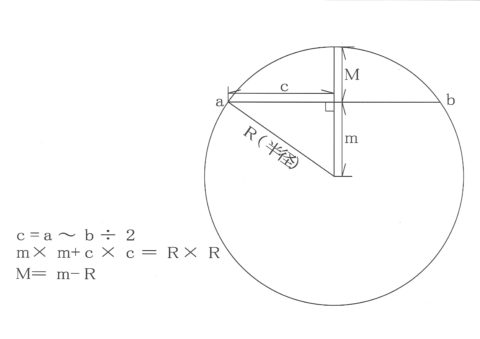
上記のM=m-Rは間違いです。すみません
正しくはM=R-mでした。
上記のように計算すれば、どんな半径でもより正確に出すことができます。
三角関数が得意ですぐ計算できる人はこちらのほうが正確なのでいいかもしれません。
道路カーブは山道でなければ基本的に半径が100m以上になりますから、最初の計算方法が楽です。
私は中学生並みの脳ミソですから、最初の計算式を使っています。三角関数なんかわすれました。
私には高性能電卓は必要ありません。なぜなら、iPhoneという強い味方にいろいろなアプリを入れてあるから、電卓たたくより早く正確に計算してくれますからw
探せば何でもある時代サイコーですね。
参考になったっと思った人はランキングのバナーのクリックをお願い致します。
ランキングに参加しています。ポチっとして応援お願いします。
![]()









コメント
こんにちわ!
小さな半径の計算のMの出し方って
M=R-√(R^2-C^2)じゃないですか?
間違ってたらすみません。
コメントありがとうございます。
うちの会社に算数しかできない人がいて、その人でもわかるようにと簡単な方法を上げています。
なるべく難しい公式を使わないでできる方法で書いていますのでご理解ください。
ちなみに
計算機での代入式
I/2=L/2R
C/2=Rsin(I/2)
M=R{1-cos(I/2)} ここで角度の単位はRAD(ラジアン)
になります。
私の書き方が分かりづらくてすみません。
単純にサイト上の表記が M=m-Rとなってしまっているので、
M=R-mの間違いではないのかという指摘です。
しっかり確認せずに返信してしまい申し訳ございません。
修正致します。
ご指摘ありがとうございます。